Bayesian regularization for RBFN
Neural Networks course (practical examples) © 2012 Primoz Potocnik
PROBLEM DESCRIPTION: 2 groups of linearly inseparable data (A,B) are defined in a 2-dimensional input space. The task is to define a neural network for solving the XOR classification problem.
Contents
- Create input data
- Define output coding
- Prepare inputs & outputs for network training
- Create a RBFN
- Evaluate network performance
- Plot classification result
- Retrain a RBFN using Bayesian regularization backpropagation
- Evaluate network performance after Bayesian regularization training
- Plot classification result after Bayesian regularization training
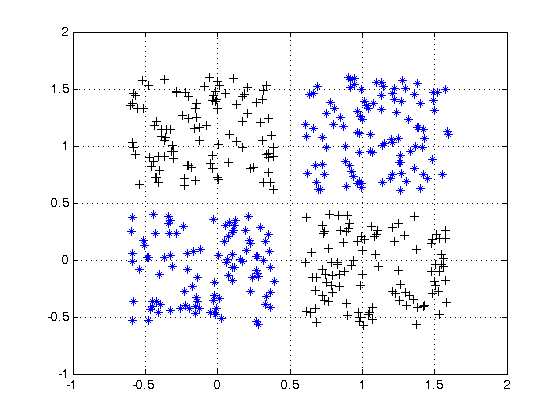
Create input data
close all, clear all, clc, format compact % number of samples of each cluster K = 100; % offset of clusters q = .6; % define 2 groups of input data A = [rand(1,K)-q rand(1,K)+q; rand(1,K)+q rand(1,K)-q]; B = [rand(1,K)+q rand(1,K)-q; rand(1,K)+q rand(1,K)-q]; % plot data plot(A(1,:),A(2,:),'k+',B(1,:),B(2,:),'b*') grid on hold on
Define output coding
% coding (+1/-1) for 2-class XOR problem
a = -1;
b = 1;
Prepare inputs & outputs for network training
% define inputs (combine samples from all four classes) P = [A B]; % define targets T = [repmat(a,1,length(A)) repmat(b,1,length(B))];
Create a RBFN
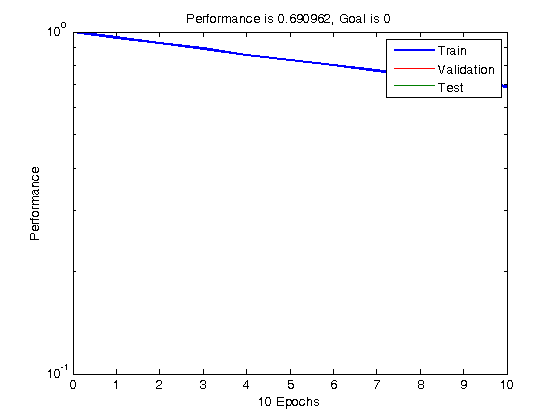
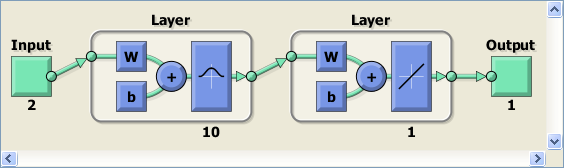
% choose a spread constant spread = .1; % choose max number of neurons K = 10; % performance goal (SSE) goal = 0; % number of neurons to add between displays Ki = 2; % create a neural network net = newrb(P,T,goal,spread,K,Ki); % view network view(net)
NEWRB, neurons = 0, MSE = 1 NEWRB, neurons = 2, MSE = 0.928277 NEWRB, neurons = 4, MSE = 0.855829 NEWRB, neurons = 6, MSE = 0.798564 NEWRB, neurons = 8, MSE = 0.742854 NEWRB, neurons = 10, MSE = 0.690962
Evaluate network performance
% check RBFN spread actual_spread = net.b{1} % simulate RBFN on training data Y = net(P); % calculate [%] of correct classifications correct = 100 * length(find(T.*Y > 0)) / length(T); fprintf('\nSpread = %.2f\n',spread) fprintf('Num of neurons = %d\n',net.layers{1}.size) fprintf('Correct class = %.2f %%\n',correct) % plot targets and network response to see how good the network learns the data figure; plot(T') ylim([-2 2]) set(gca,'ytick',[-2 0 2]) hold on grid on plot(Y','r') legend('Targets','Network response') xlabel('Sample No.')
actual_spread =
8.3255
8.3255
8.3255
8.3255
8.3255
8.3255
8.3255
8.3255
8.3255
8.3255
Spread = 0.10
Num of neurons = 10
Correct class = 79.50 %
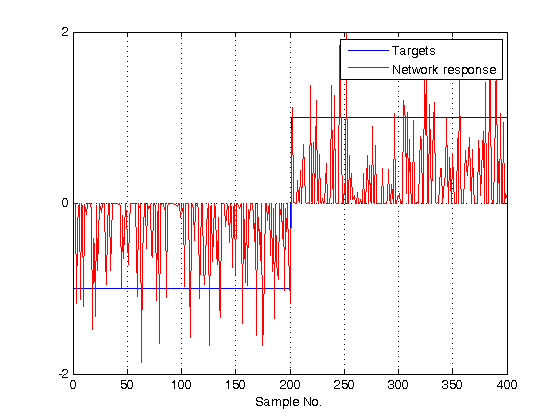
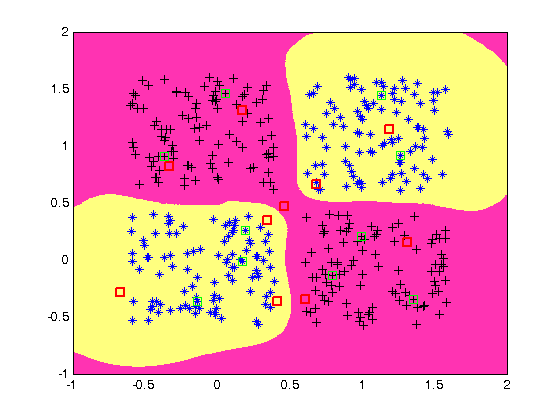
Plot classification result
% generate a grid span = -1:.025:2; [P1,P2] = meshgrid(span,span); pp = [P1(:) P2(:)]'; % simualte neural network on a grid aa = sim(net,pp); % plot classification regions based on MAX activation figure(1) ma = mesh(P1,P2,reshape(-aa,length(span),length(span))-5); mb = mesh(P1,P2,reshape( aa,length(span),length(span))-5); set(ma,'facecolor',[1 0.2 .7],'linestyle','none'); set(mb,'facecolor',[1 1.0 .5],'linestyle','none'); view(2) % plot RBFN centers plot(net.iw{1}(:,1),net.iw{1}(:,2),'gs')
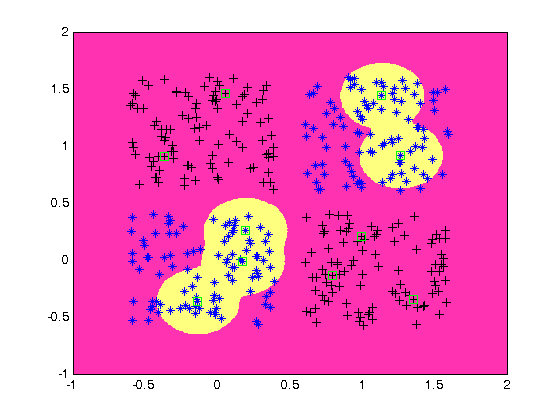
Retrain a RBFN using Bayesian regularization backpropagation
% define custom training function: Bayesian regularization backpropagation net.trainFcn='trainbr'; % perform Levenberg-Marquardt training with Bayesian regularization net = train(net,P,T);
Evaluate network performance after Bayesian regularization training
% check new RBFN spread spread_after_training = net.b{1} % simulate RBFN on training data Y = net(P); % calculate [%] of correct classifications correct = 100 * length(find(T.*Y > 0)) / length(T); fprintf('Num of neurons = %d\n',net.layers{1}.size) fprintf('Correct class = %.2f %%\n',correct) % plot targets and network response figure; plot(T') ylim([-2 2]) set(gca,'ytick',[-2 0 2]) hold on grid on plot(Y','r') legend('Targets','Network response') xlabel('Sample No.')
spread_after_training =
2.9924
3.0201
0.7809
0.5933
2.6968
2.8934
2.2121
2.9748
2.7584
3.5739
Num of neurons = 10
Correct class = 100.00 %
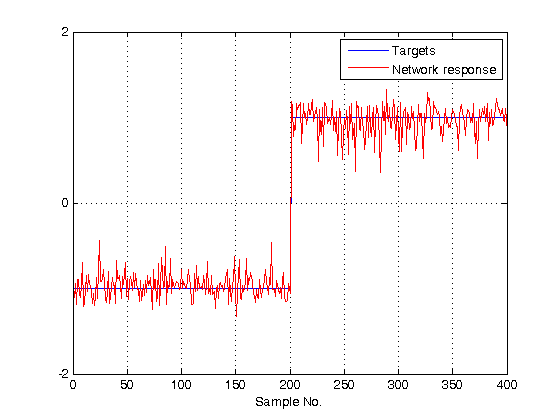
Plot classification result after Bayesian regularization training
% simulate neural network on a grid aa = sim(net,pp); % plot classification regions based on MAX activation figure(1) ma = mesh(P1,P2,reshape(-aa,length(span),length(span))-5); mb = mesh(P1,P2,reshape( aa,length(span),length(span))-5); set(ma,'facecolor',[1 0.2 .7],'linestyle','none'); set(mb,'facecolor',[1 1.0 .5],'linestyle','none'); view(2) % Plot modified RBFN centers plot(net.iw{1}(:,1),net.iw{1}(:,2),'rs','linewidth',2)