Calculation and plot of the poincare section of two uncoupled osciators with omega1 and omega2 : omega1/omega2=p/q=rational -> closed orbit, periodic behaviour; omega1/omega2=irational -> quasiperiodic behaviour

Contents

close;
clear;
ps=zeros(2,1);

integration of torus.m

[t,y]=ode45(@torus,[0:0.001:100],[0.5 0.5 0.5]);
%plot projection of the phas space orbit to y1-y2 plane
plot(y(:,1),y(:,2));
hold;

Current plot held

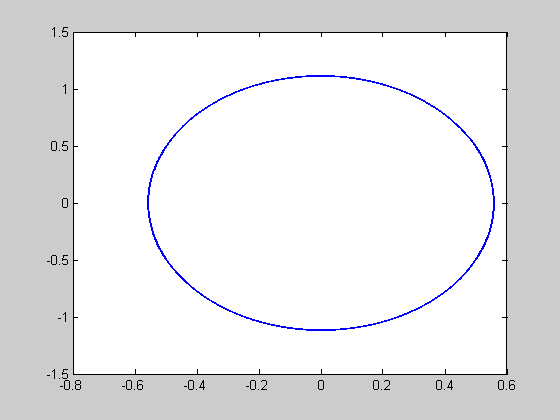
calculation of poincare section

calculate number of integration steps

n=size(t);
%set the index of poincare points to 1
np=1;
for i=1:n(1)
        % detect the cros-section of the trajectory with the plane y1-y2
        if(y(i,3)>=(2*pi)*np)
            % store detected cross-section point y1,y2 to ps1,ps2
        ps(np,1)=y(i,1);
        ps(np,2)=y(i,2);
        % increase the index of poincare point
                np=np+1;
        end
end

plot the poincare section

for i=1:np-1
    plot(ps(i,1),ps(i,2),'r+')
    % use pause to folow the plot of the poincare section
    %pause(2);
    end
%plot(ps(:,1),ps(:,2),'r+');

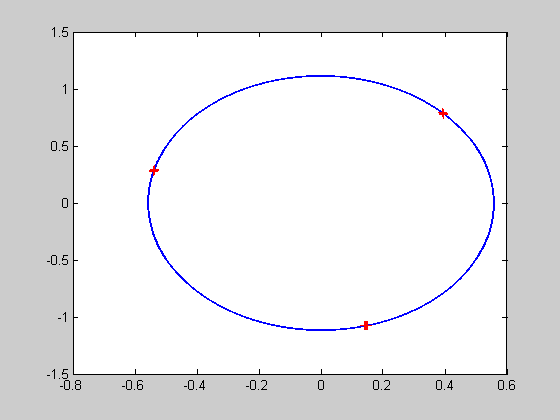
torus.m file - two uncoupled oscilators with omega1=2 and omega2=3

%function dy=torus(t,y)
%dy=zeros(3,1);
%dy(1)=y(2);
%dy(2)=-(omega1)*y(1);
%dy(3)=omega2;

Published with MATLAB® 7.5